SDMs : Schrödinger Distribution Models

Tout le monde connait le chat de Schrödinger.

Ce fameux chat qui serait à la fois mort et vivant, tel que défini d’après un modèle quantique.

On peut s’amuser à faire l’analogie avec les prédictions d’impacts des changements climatiques sur les répartitions d’espèces. La plupart de ces prédictions ont été réalisées par le biais des modèles de prédictions de répartition (abrégés SDMs en anglais). Le problème, c’est que les SDMs sont des techniques assez incertaines.

Petite définition technique

Techniquement, les SDMs consistent à corréler l’occurrence d’une espèce (les lieux où elle a été observée) à des variables environnementales (par exemple le climat connu dans ces lieux). Cela nous permet de supposer la relation entre espèce et environnement, et ainsi d’extrapoler dans l’espace pour voir où l’environnement est favorable à la présence de l’espèce ; et dans le temps, par exemple pour prédire les impacts des changements climatiques sur l’espèce.

D’une part, il existe de nombreuses techniques différentes (« GLM », « GAM », « MaxEnt », « BRT », etc.) ; chacune avec leurs propres hypothèses sous-jacentes, et paramétrisations. Ces différentes techniques donnent souvent des résultats différents, parfois même divergents. De plus, il existe de nombreux protocoles : basés sur les données de présence-absence, de présence seulement avec échantillonnage de pseudo-absences (sous différentes modalités), de validation croisée, etc.

Il faut également bien choisir ses variables environnementales, pour qu’elles soient pertinentes. Quand on connait bien la biologie de l’espèce, ça peut être facile, mais quand ce n’est pas le cas, on essaye  de les identifier par un protocole de sélection de variables. Différentes variables sélectionnées impliquent différents résultats.

A cela s’ajoute le fait que pour faire des projections dans le futur, il faut se baser sur des scénarios, qui sont donc incertains. Et pour chacun de ces scénarios, il y a de nombreux modèles climatiques, chacun tentant de représenter à sa manière le climat futur pour le scénario associé. Ils sont tous plus ou moins performants, chacun étant plus fort dans une région du globe que dans une autre. Comme prévu donc, différents modèles climatiques donnent des résultats différents pour un même scénario.

J’omets ici de parler des données d’occurrence de l’espèce que l’on cherche à modéliser : suivant leur quantité et qualité (enfin, plutôt leurs biais), les résultats seront également différents.

Comment choisir le bon modèle ?

On pourrait utiliser les techniques d’évaluation des modèles, pour tenter de trouver le meilleur modèle. Cependant, ces techniques permettent rarement de « réellement » évaluer les modèles (je ne m’étale pas dessus dans cet article, ce sera peut-être le sujet d’un future article). Ainsi, en général, les techniques d’évaluation ne permettent pas d’identifier les prédictions fiables ; elles permettent seulement d’évaluer les prédictions non fiables. En d’autres termes : une mauvaise évaluation d’un modèle signifie que le modèle est très certainement très mauvais ; par contre une bonne évaluation ne signifie pas que le modèle est bon.

Nous restent alors les approches de type modélisation d’ensembles (Ensemble Modelling), qui consistent à faire nos prédictions avec différentes techniques de modélisation, différents modèles climatiques, etc. puis de regarder la prédiction moyenne, ou médiane. Plusieurs travaux ont montré que cette prédiction moyenne ou médiane donnait de meilleurs résultats qu’une prédiction individuelle ; mais la véritable force de l’Ensemble Modelling est de montrer la variabilité des prédictions.  Si toutes nos prédictions sont les mêmes, le résultat est bien plus fiable que lorsque les prédictions sont opposées !

Schrödinger Distribution Models

Cependant, si on ose regarder l’ensemble de nos prédictions, il n’est pas rare d’aboutir à des ‘Schrödinger Distribution Models‘, avec la même espèce prédite pour à la fois s’éteindre (-100% à la taille de son aire de répartition) et se super-étendre (par exemple, +200% à la taille de son aire) !

Ces Schrödinger Distribution Models posent deux questions :

1. Peut-on faire confiance à une prédiction livrée sans incertitude ?

2. Comment utiliser des prédictions dignes de Schrödinger ?

1. Une prédiction sans incertitude est incertaine

Les SDMs sont donc incertains, d’autant plus dans le cas des projections futures. Pour cette raison, il m’apparait indispensable de donner une indication de l’incertitude du résultat lorsque l’on fait des prédictions. Interpréter sans incertitude relève de l’horoscope.Il faut de toute évidence présenter les résultats de différents scénarios de changement climatique, car ce sont différents futurs plausibles identifiés par le GIEC. Mais il faut également informer de la variabilité des prédictions en réalisant un ‘ensemble model’ par scénario, montrant toutes les prédictions possibles pour ce scénario.

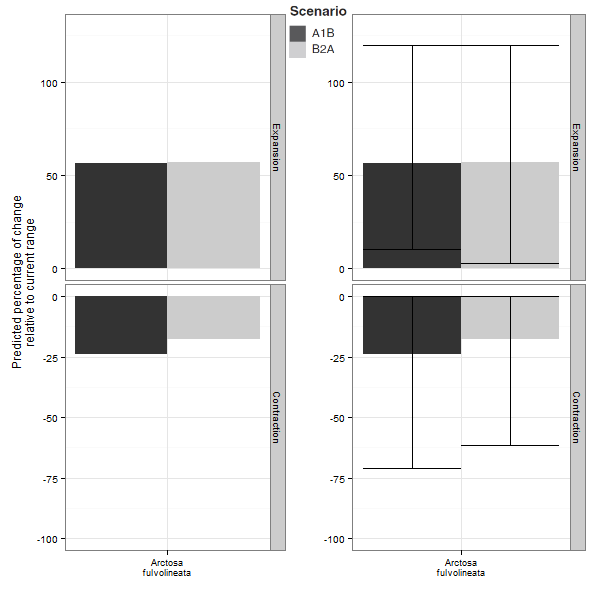
Ci-dessous, un exemple tiré d’un article que l’on a récemment publié sur les araignées. A gauche, les prédictions moyennes issues de l’ensemble modelling fournies seules ; à droite, les prédictions moyenne fournies avec leurs incertitudes (intervalles représentant 95% des prédictions). L’expansion d’aire prédite dans le futur va donc de +0% à +125%, tandis que la contraction prédite va de -0% à -75%. On constate donc que si on se base sur la seule prédiction moyenne, cela revient à se passer de la majeure partie de l’information.

Dans le cas de l’utilisation d’une seule prédiction pour un scénario climatique,  celle-ci devrait être solidement justifiée, sinon il devient possible de choisir la prédiction qui nous arrange le mieux, celle qui donne le résultat que l’on attendait…

2. Une prédiction incertaine peut donner des certitudes — ou comment utiliser des prédictions dignes de Schrödinger ?

D’une part, des modèles totalement en désaccord nous donnent la certitude de la piètre qualité des prédictions. Elle conduit à se poser des questions sur la qualité de la calibration, sur les raisons pour lesquelles les résultats des modèles ne convergent pas. On peut avoir affaire à une espèce dont la répartition est en réalité conditionnée par des facteurs trop difficiles à modéliser (par les SDMs), tels que des facteurs à des micro-échelles, des facteurs biotiques, etc.

D’autre part, selon la question posée, il est également possible d’exploiter des prédictions très divergentes en « s’extrayant » de l’incertitude issue des modèles. Kujala et al. (2013) proposent par exemple un cadre méthodologique robuste pour planifier des actions de conservation sur la base de prédictions incertaines. Pour résumer, le principe consiste à se concentrer sur les régions où les modèles sont d’accord, plutôt que celles où les modèles sont en désaccord.

Par exemple, il est possible de calculer une probabilité de présence « dépourvue d’incertitude », en soustrayant de la probabilité moyenne (de l’ensemble modelling) n fois l’écart-type des probas de présence issues de toutes les prédictions. Ce type d’approche est tiré des théories de décision face à des incertitudes sévères, et à mon avis il serait bénéfique qu’elles se généralisent dans le cadre des prédictions des impacts des changements globaux sur la biodiversité. C’est ce que nous avons fait sur les araignées pour identifier des populations à protéger dans le cadre d’un programme de conservation, malgré une incertitude élevée pour certaines espèces.

TL; DR

Les modèles de prédiction de répartition ont des incertitudes inhérentes qui peuvent être énormes dans le cadre de projections futures : ces incertitudes devraient toujours être évaluées pour interpréter correctement.

Ne croyez jamais une prédiction livrée sans indications d’incertitude…

Des méthodes existent pour pouvoir utiliser les SDMs malgré des incertitudes énormes, et devraient donc être (systématiquement ?) appliquées.